LeetCode: 145 Binary Tree Postorder Traversal

0145 Binary Tree Postorder Traversal

Problem Description

Given the root of a binary tree, return the postorder traversal of its nodes' values.

Example

Input: root = [1,null,2,3]
Output: [3,2,1]

Solution

Please refer this post for more details on the BST and traversal methods. Using recursive method is trivial after you solved the Inorder Traversal Problem and Preorder Traversal Problem, while we want to point out that iterative and Morris methods need moderate modifications in order to have a correct working code for this Postorder traversal problem.

Recursive Method

The simplest solution.

vector<int> ret;
vector<int> postorderTraversal(TreeNode* root) { // recursively
        postorder(root);
        return ret;
    }
    
    void postorder(TreeNode* root){
        if(!root) return;
        postorder(root->left);
        postorder(root->right);
        ret.push_back(root->val);
    }

Iterative Method with stack

Postorder will scan the leaves first and go to their parent nodes. So you will print the value of a node only when it is a leaf (no left or right child) or its children have already been printed. Following this, you may write out the iterative code with the experience from the inorder or preorder problem. Just note that you will need addition variable pre to help avoiding visiting a node more than one time.

vector<int> postorderTraversal(TreeNode* root) { // iteratively
        vector<int> ret;
        stack<TreeNode*> stk;
        TreeNode* pre=nullptr;
        while(root || !stk.empty()){
            while(root){
                stk.push(root);
                root = root->left;
            }
            root = stk.top();
            if(root->right && root->right!=pre) root = root->right;
            else{
                stk.pop();
                ret.push_back(root->val);
                pre = root;
                root = nullptr;
            }
        }
        return ret;
    }

Iterative Method with stack 2

We also provide a second version of iterative method on this problem. If you find it not so easy to come up the above code, you could consider this one. The idea is simple, remember the postorder is:[left, right, root], let's say if we reverse the order, it will be :[root, right, left]. Observe it is very similiar to a preorder scan except we have [right, left] instead of [left, right]. But it's easy: simply replace left(right) with right(left) in the code. Then finally you reverse the vector before the printout.

vector<int> postorderTraversal(TreeNode* root) { // "preorder" + output reverse
        vector<int> ret;
        stack<TreeNode*> stk;
        TreeNode* pre=nullptr;
        while(root || !stk.empty()){
            while(root){
                stk.push(root);
                ret.push_back(root->val);
                root = root->right;
            }
            root = stk.top();
            stk.pop();
            root = root->left;
            
        }
        return vector(ret.rbegin(), ret.rend());
    }

Morris Method

In order to solve the problem with the Morris method, we had better understand clearly what it is doing: it will add additional links (green) to tunnel between the leaf with its grand-parent node. And the curr pointer will move along the blue curve shown in the graph. As you can see we will always visit the node with left children twice, but fortunately we can distinguish these two cases. Another observation is that the blue curve flows from parent to its children, while postorder wants to go from children to parents. So we need to somehow reverse the prinout. The idea of code below: when we visit the node the second time, we print its first left child and its following right children: for example when we visit the node 1 again, we go to its left child that is node 2 and start to print it right down to the node 5. But then we need to reverse the order of [2,4,5] to [5,4,2]. See the code for details.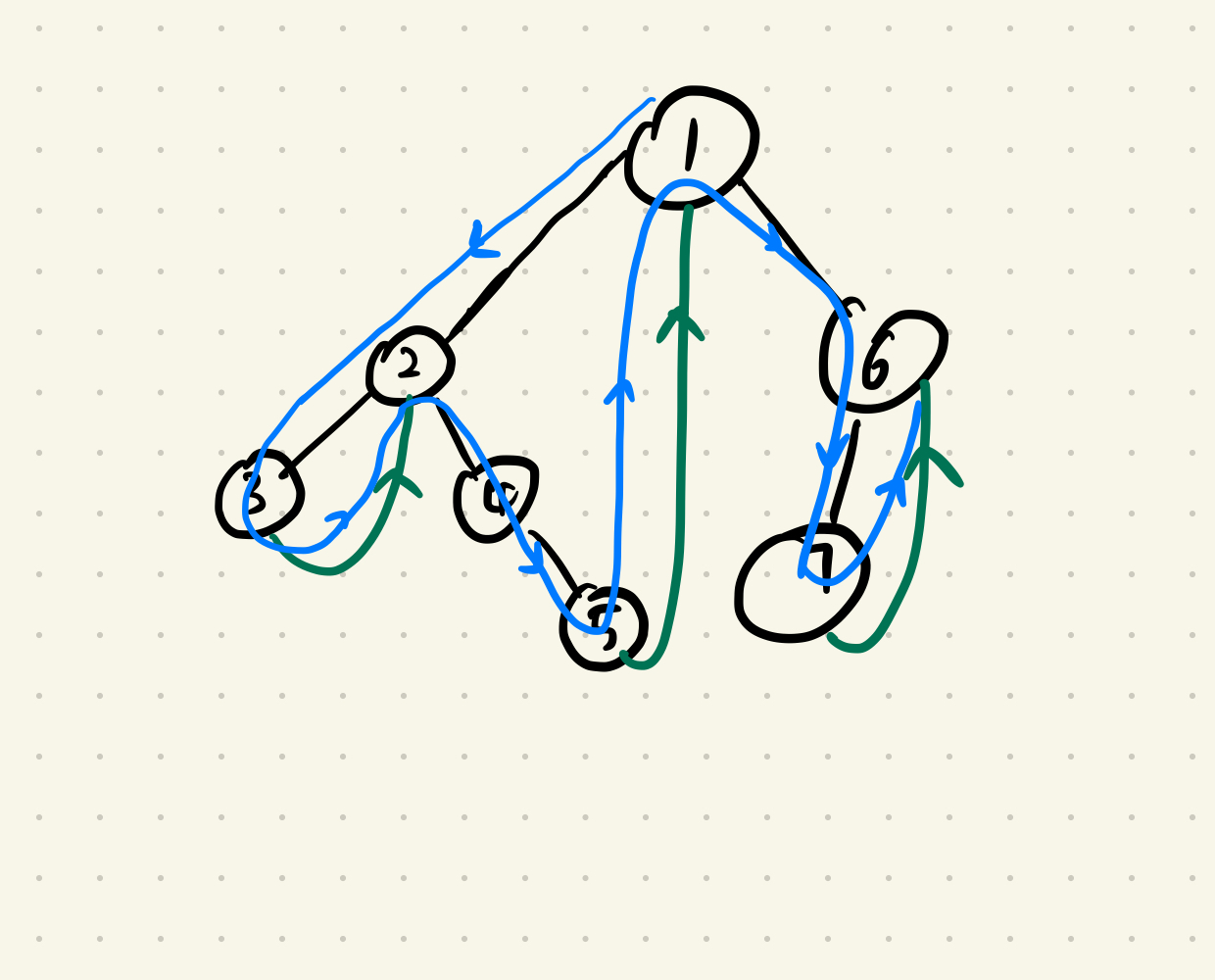

vector<int> ret;
    void addPath(TreeNode* root){
        int cnt=0;
        while(root){
            ret.push_back(root->val);
            root = root->right;
            cnt++;
        }
        reverse(ret.end()-cnt, ret.end());
    }
    vector<int> postorderTraversal(TreeNode* root) { // Morris method
        TreeNode *curr = root, *pre=nullptr;
        while(curr){
            pre = curr->left;
            if(pre){
                while(pre->right && pre->right!=curr) pre = pre->right;
                if(!pre->right){
                    pre->right = curr;
                    curr = curr->left;
                }else{
                    pre->right = nullptr;
                    addPath(curr->left);
                    curr = curr->right;
                }
            }else curr = curr->right;
        }
        addPath(root);
        return ret;
    }